The Liquid State Machine Framework

This page briefly describes the basic conecpts of the LSM framework. For a more in depth treatment of this issue see (Maass et al., 2002) and (Natschläger et al., 2002). The same basic ideas where independently described in (Jaeger, 2001) from an engineering point of view (for more info see the Echo State Networks Homepage).

The conceptual framework of a Liquid State Machine (LSM) facilitates the analysis of the real-time computing capability of neural microcircuit models. It does not require a task-dependent construction of a neural circuit, and hence can be used to analyze computations on quite arbitrary ``found'' or constructed neural microcircuit models. It also does not require any a-priori decision regarding the ``neural code'' by which information is represented within the circuit.

Temporal Integration

The basic idea is that a neural (recurrent) microcircuit may serve as an unbiased analog (fading) memory (informally referred to as ``liquid'') about current and preceding inputs to the circuit.

The ``liquid state''

We refer to the vector of contributions of all the neurons in the microcircuit to the membrane potential at time t of a generic readout neuron as the liquid state x(t). Note that this is all the information about the state of a microcircuit to which a readout neuron has access. In contrast to the finite state of a finite state machine the liquid state of an LSM need not be engineered for a particular task. It is assumed to vary continuously over time and to be sufficient sensitive and high-dimensional that it contains all information that may be needed for specific tasks.

Memoryless readout map

The liquid state x(t) of a neural microcircuit can be transformed at any time t by a readout map f into some target output f(x(t)) (which is in general given with a specific representation or neural code).

The Liquid State Machine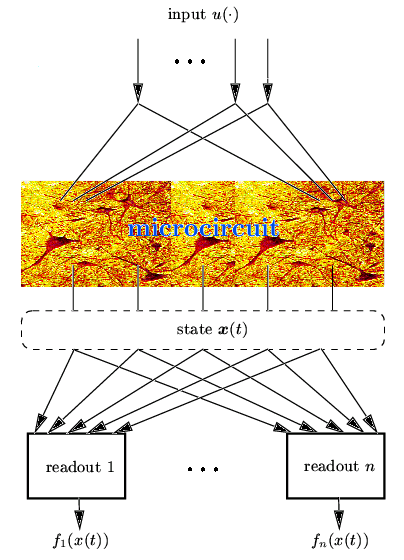

Figure 1. The Liquid State Machine (LSM). The recurrent microcircuit (liquid) transforms the input into states x(t), which are mapped by the memory-less readout functions f₁, ..., f_n to the outputs f₁(x(t)), ..., f_n(x(t)).

Separation Property

We will argue that only the synapses of these readout neurons have to be adapted for a particular computational task. This requires that any two different input time series u(s), s ≤ t and v(s), s ≤ t which should produce different outputs at some subsequent time t put the recurrent circuit into two (significantly) different states x_u(t) and x_v(t) at time t. In other words: the current state x(t) of the microcircuit at time t has to hold all information about preceding inputs.

Offline training of a readout function

If the liquid has this property it is possible to train a memory-less readout to produce the desired output at time t. If one lets t vary, one can use the same principles to produce as output a desired time series or function of time t with the same readout unit. This yields the following (offline) procedure for training a readout to perform a given task based on the ideas sketched above.

1. Define the neural microcircuit to be analyzed
2. Record states x(t) of the microcircuit at various time points in response to numerous different (training) inputs u(×)
3. Apply a supervised learning algorithm to a set of training examples of the form [x(t),y(t)] to train a readout function f such that the actual outputs f(x(t)) are as close as possible to the target outputs y(t).

One advantage of this approach is that it is not necessary to take any temporal aspects into account for the learning task, since all temporal processing is done implicitly in the recurrent circuit. Furthermore no a-priori decision is required regarding the neural code by which information about preceding inputs is encoded in the current liquid state of the circuit. Note also that one can easily implement several computations in parallel using the same recurrent circuit. One just has to train for each target output a separate readout neuron, which may all use the same recurrent circuit.

Universal computational capabilities

According to the theoretical analysis of this computational model, see (Maass et al., 2002), there are no a-priori limitations for the power of this model for real-time computing with fading memory. Of course one needs a larger circuit to implement computations that require more memory capacity or more noise-robust pattern discrimination.

Benchmark Tests

The theoretically predicted universality of this computational model for neural microcircuits can not be tested by evaluating their performance for a single computational task. Instead, each microcircuit model should be tested on a large variety of computational ``benchmark tasks''.

Echo State Networks

Independently the basic ideas of the LSM framework have been investigated by H. Jaeger from an engineering point of view (Jaeger, 2002). In that work artificial recurrent neural networks have been used as a ``liquid'' and linear readout functions have been trained to fulfill several different tasks (for more info go to the EchoState Networks Page).